Searching and Sorting
Binary Search
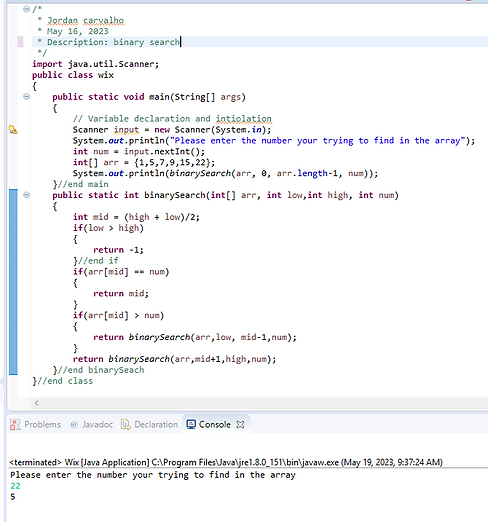
Binary search is an efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing in half the portion of the list that could contain the item, until you've narrowed down the possible locations to just one.
In the example you will see me asking the user for the number there trying to find in the array and reclusively going though the array, eliminating until I find the number.
*Note: Array has to be SORTED*
Linear Search
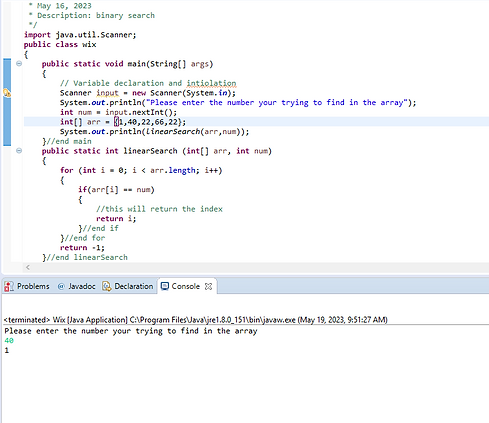
Linear Search is very ineffective way to find an element in an array. It will start at index 0 check if it equals the number your trying to find. If it does not equals it will check at index 1, etc:
Advantage to this code is that the array does not have to be sorted.
If you look at the example to your right your will see the code.

Bubble Sort
Bubble sort is the easiest way to sort, but very inefficient.
For example: We have the array [6,3,0,5]
ordering from least to greatest
First Pass:
-
Bubble sort starts with very first two elements, comparing them to check which one is greater.
-
( 6 3 0 5 ) –> ( 3 6 0 5 ), Here, algorithm compares the first two elements, and swaps since 6 > 3.
-
( 3 6 0 5 ) –> ( 3 0 6 5 ), Swap since 6 > 0
-
( 3 0 6 5 ) –> ( 3 0 5 6 ), Swap since 6 > 5
-
Second Pass:
Now, during second iteration it should look like this:
( 3 0 5 6 ) –> ( 0 3 5 6 ), Swap since 3 > 0
( 0 3 5 6 ) –> ( 0 3 5 6 ), No change as 5 > 3
Third Pass:
Now, the array is already sorted, but our algorithm does not know if it is completed.
The algorithm needs one whole pass without any swap to know it is sorted.
( 0 3 5 6 ) –> ( 0 3 5 6 ), No change as 3 > 0
Array is now sorted and no more pass will happen.
Selection Sort
If trying to sort from smallest to greatest: Selection Sort is when it will go through a list of numbers that are unsorted and will find the lowest and move to the front of the array sorted.
If you look at the example on your left. Here you will see a virtual image of the code prosses. If you click you will see the code.
Insertion sort
-
This algorithm is one of the simplest algorithm with simple implementation
-
Basically, Insertion sort is efficient for small data values
-
Insertion sort is adaptive in nature, i.e. it is appropriate for data sets which are already partially sorted.
On the imagine of the left shows how the array will be sorted by insertion sort. The array starts at [4,3,2,10,12,1,5,6].
If you click the imagine you will see the code for insertion sort
Merge Sort
In simple terms, we can say that the process of merge sort is to divide the array into two halves, sort each half, and then merge the sorted halves back together. This process is repeated until the entire array is sorted.
If you look at the image on the right you will see how the code is suspose to work.
Merge Sort is one of the quickest ways to sort an array. The disadvantage of is that it takes up a lot of sortage.
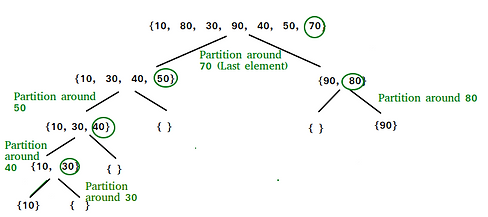
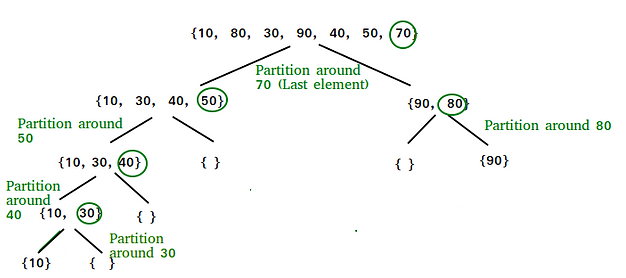
Quick Sort
The key process in quickSort is a partition(). The target of partitions is to place the pivot (any element can be chosen to be a pivot) at its correct position in the sorted array and put all smaller elements to the left of the pivot, and all greater elements to the right of the pivot.
This partition is done recursively which finally sorts the array. See the image on the left for a better understanding.
If you will click on the image you will see the code.
